Πώς είναι το καταστροφικό πιστόλι της Misaka;

[Unboxing - BBB] 베이 블레이드 버스트 超王 (슈퍼 킹) 리뷰 3 - B-161 [부스터] 글라이드 라그나 뢰크 .Wh.R 1S 리뷰 & 테스트

Στο επεισόδιο 1 του Railgun, το railgun του Misaka καταλήγει σε ένα καλό κομμάτι από αυτό που φαίνεται να είναι πισίνα ολυμπιακού μεγέθους. Αργότερα στο ίδιο επεισόδιο, αποκαλύπτεται ότι το railgun της ταξιδεύει με ταχύτητα 1030 m / s.

Ωστόσο, οι αριθμοί δεν αυξάνονται.

Ας υποθέσουμε ότι η Misaka χρησιμοποιεί κέρματα 10 γραμμαρίων. Στο 1030 m / s, αυτό το νόμισμα έχει τόσο μεγάλη ενέργεια:

Energy = 1/2 m v^2 = 1/2 (0.01 kg) (1030 m/s)^2 = 5304.5 kg (m/s)^2 = 5304.5 Joules

Μια πισίνα ολυμπιακού μεγέθους έχει 2.500.000 κιλά νερό. Με βάση την παραπάνω εικόνα, αυτός ο κώνος ταξιδεύει πιθανώς 100 μέτρα στον αέρα.

Ας πούμε λοιπόν για την αμφιβολία ότι μόνο 10% του νερού ανυψώνεται 100 μέτρα στον αέρα.

Energy = m g h = (0.01 * 2500000 kg) (9.8 m/s^2) (100 m) = 2.45 * 10^8 kg (m/s)^2 = 2.45 * 10^8 Joules

Το νόμισμα χρειάζεται 2.45 * 10^8 Joules ενέργειας για την ανύψωση της πισίνας όπως φαίνεται παραπάνω. Αλλά το νόμισμά της μπορεί να προσφέρει μόνο 5304.5 Joules. Υπάρχει μια διαφορά περίπου 4 τάξεων μεγέθους.

Εντάξει ... Πριν κάποιος το απορρίψει ως μια άλλη περίπτωση της φυσικής Anime, ας δούμε τι άλλο θα μπορούσε να παράγει τόση ενέργεια:

Η περιστροφή του νομίσματος δεν καταγράφεται στην καθαρή ταχύτητα των 1030 m / s. Αλλά δεδομένης της στιγμής της αδράνειας ενός μικρού νομίσματος, θα χρειαζόταν ένα τεράστιο (σχετικιστικό;) ποσό περιστροφής για να μεταφέρει 10^8 Τζουλς.
Η χρέωση του νομίσματος δεν έχει καθοριστεί στο Anime. Ίσως ο Misaka να πολώνει με κάποιο τρόπο τη χρέωση στο νόμισμα και με κάποιο τρόπο να την απελευθερώνει κατά την επαφή με τον στόχο.
Η μαζική ενέργεια (E = mc^2) του νομίσματος είναι 9 * 10^14 Τζουλς. Είναι αυτό που έκανε;

Το ερώτημα λοιπόν είναι: Υπάρχει κάποια επίσημη εξήγηση για το πού παίρνει το νόμισμα τόση ενέργεια; Ή μήπως αφήνεται να το απορρίψουμε ως άλλη περίπτωση της φυσικής Anime;

Και αν κάποιος ενδιαφέρεται για τη συζήτηση για τη φυσική εδώ: chat.stackexchange.com/transcript/message/7951592#7951592
FWIW, Funimation έγραψε μια ανάρτηση ιστολογίου, μια συγκεκριμένη επιστημονική εξήγηση των Railguns, πέρυσι. Δυστυχώς, το συνδεδεμένο PDF που έτρεξε τους αριθμούς και λάμπει πόσο λάθος φαίνεται να έχει χαθεί. IIRC, οι απαντήσεις εδώ καλύπτουν ήδη όλα όσα είπε.
@Mystical by Official εννοείτε μια καθαρά φυσική εξήγηση ή μια κανονική εξήγηση;
@Mindwin Με "Επίσημο" εννοώ αν το στούντιο ή κάποιος από τους συγγραφείς έχει πει κάτι.

Σύμφωνα με το anime και το manga, το Mikoto έχει "ταχύτητα ρύγχους" 1030 m / s:

Αντίθετα, το πιστόλι του Πολεμικού Ναυτικού των ΗΠΑ έχει ταχύτητα ρύγχους 2520 m / s (~ 5600 mph ή ~ 7.5x την ταχύτητα του ήχου), με ενέργεια ρύγχους 10,64 megajoules (10,64 εκατομμύρια joules). Το οποίο είναι πιθανώς συγκρίσιμο με την ποσότητα ενέργειας σε ένα αυτοκίνητο μέσου μεγέθους που κινείται στα 250 mph.

Συγκριτικά, το τουφέκι AK-47 έχει ταχύτητα ρύγχους 715m / s (~ 1600 mph ή ~ 2x την ταχύτητα του ήχου), με ενέργεια ρύγχους ~ 2010 joules (υποθέτοντας ότι χρησιμοποιούνται φυσίγγια 7,62x39mm, αλλά μπορεί να διαφέρει ανάλογα με τον τύπο των πυρομαχικών).

Παρόλο που δεν είναι πολύ εντυπωσιακό, όσο οι σιδηροτροχιές, οι πραγματικές σιδηροτροχιές είναι σε θέση να επιτυγχάνουν ταχύτητες πιθανώς μεγαλύτερες από ~ 5000 m / s. Λάβετε υπόψη ότι το Mikoto είναι μαθητής μέσης εκπαίδευσης που μπορεί να πυροβολήσει οκτώ βολές ανά λεπτό, κάτι που είναι ισοδύναμο με τα «τυπικά» όπλα.

Υποθέτοντας ότι το κέρμα συγκρίνεται με το μέγεθος και το βάρος ενός αμερικανικού τετάρτου, μπορεί κανείς να υποθέσει ότι το νόμισμα που χρησιμοποιεί έχει βάρος περίπου πέντε γραμμάρια. Χρησιμοποιώντας αυτήν τη φόρμουλα μπορούμε να κάνουμε το ρύγχος της ενέργειας:

Ενέργεια = 0,5 * (μάζα) (ταχύτητα)² = 0,5 * (0,005kg) (1030m / s)² = ~ 2652,25 joules

Έτσι, το Mikoto προκαλεί λίγο μεγαλύτερη ζημιά από ένα ημιαυτόματο τουφέκι.

Αλλά αυτό δεν βλέπουμε τώρα είναι έτσι;

ΟΧΙ ακριβως. Αλλά τι θα μπορούσε να προκαλέσει μια τέτοια διαφορά στην παραγωγή;

Σύμφωνα με τη σελίδα 1, Κεφάλαιο 4 του manga Railgun, χειρίζεται τον ηλεκτρομαγνητισμό για να επιτύχει τα αποτελέσματά της. Αυτό φαίνεται εύλογο, εφόσον εάν το μαγνητικό πεδίο ήταν επαρκώς εστιασμένο, θα μπορούσε θεωρητικά να επιταχύνει μόνο το νόμισμα ή / και τα κοντινά αντικείμενα.

Τώρα ας ρίξουμε μια ματιά στη δοκιμή πισίνας ξανά, από το επεισόδιο καθαρισμού πισίνας (S1, επ. 2) έχουμε μια κατά προσέγγιση εκτίμηση των διαστάσεων της πισίνας:

Ας μετρήσουμε τα πράγματα από την άποψη του ύψους Kuroko (~ 152cm)!

Βλέποντας ότι η πισίνα δεν μειώνεται ή ούτε στα άκρα, ας υποθέσουμε ότι η πισίνα έχει μήκος περίπου 14 Kurokos ή ~ 21,28 m (ναι φαίνεται κάπως μικρή), και περίπου 11 Kurokos πλάτος, ή ~ 16,72 m, από τις γραμμές το πάτωμα της πισίνας και λίγο λιγότερο από ~ 0,9 Kuroko, ή ας πούμε βάθος 1,36μ.

Όσο για το εκτοπισμένο νερό, εμείς θα μπορούσε προσπάθεια ενσωμάτωσης του όγκου του νερού, υποθέτοντας ότι είναι μισός και μισός αέρας, βρίσκουμε το βάρος του, κ.λπ. Αλλά θα είμαστε τεμπέλης εδώ και θα υποθέσουμε ότι το 1/1000 του όγκου νερού της πισίνας διασκορπίστηκε στον αέρα όταν πυροδοτεί το Mikoto το πιστόλι της. Η πισίνα θα είχε έναν όγκο:

Όγκος = (1,36 m) * (21,28 m) * (16,72 m) = ~ 486,73 m³ από νερό

Δεδομένου ότι το "κέντρο μάζας" φαίνεται ότι το λοφίο του νερού είναι συγκρίσιμο να βρίσκεται κοντά στην κορυφή του κτηρίου τύπου γυμναστηρίου, θα είναι μια εκτίμηση ματιών της πόρτας σε σύγκριση με το κτίριο ας υποθέσουμε ότι έχει ύψος 10 μέτρα. Για να υπολογίσουμε την ενέργεια που απαιτείται για να πετύχουμε κάτι τέτοιο κάνουμε:

(Ενέργεια που απαιτείται για την ανύψωση ενός αντικειμένου) = (μάζα αντικειμένου) * (επιτάχυνση λόγω βαρύτητας) * (υψόμετρο ανύψωσης).

Σε αυτό το σενάριο ας κόψουμε πολλές γωνίες και ας υποθέσουμε ότι όλη η ενέργεια του πυροβολισμού πηγαίνει στην ανύψωση του νερού (με την οποία αγνοούμε την ενέργεια που δαπανάται για τη θέρμανση του νερού, δημιουργώντας τους ήχους δυνατής έκρηξης, τυχόν δραματική επίδραση ανέμων), τότε εμείς έχω

Ενέργεια = (1/1000) * (~ 486,73 m³) * (1000 kg / m³ νερό) * (9,8 m / s²) * (10m) = ~ 47699,54 joules

Εάν το συνδέσουμε προς τα πίσω στην εξίσωση κινητικής ενέργειας:

√ [(~ 47699,54 J) * 2 / (0,005 kg)] = ~ 4368,04 m / s

Έτσι, η ταχύτητα του ρύγχους της κάγκελός της θα ήταν ~ 4368,04 m / s.

Κάποιος μπορεί να υποθέσει ότι, δεδομένου ότι πρέπει να σεβόμαστε την τιμή των 1030 m / s, ότι ίσως η ζημιά που προκαλείται από την ικανότητα του Mikoto οφείλεται στον χειρισμό της ηλεκτρομαγνητικής που προκαλείται καθώς το νόμισμα κινείται μέσω του αέρα ή κάποιον άλλο παράγοντα ... Αλλά και πάλι, τι ξέρουμε για τη φυσική αυτού του κόσμου όπου συνυπάρχουν η Επιστήμη και η Μαγεία;

Το @Krazer από την εμφάνιση του, μοιάζει με μια ημι-ολυμπιακή πισίνα, 25m x 12,5m x 1,36m

+100

Η ηλεκτρική ενέργεια μπορεί να μετακινήσει το νερό:

Το wiki λέει ότι η Misaka μπορεί να παράγει 1 δισεκατομμύριο βολτ.
(παρόλο που ορισμένες πηγές δηλώνουν 5 δισεκατομμύρια βολτ, ας είμαστε ΜΟΝΤΕΣ )

Εάν χρεώσει το νόμισμα, η ταχεία μεταφορά φορτίου από το νόμισμα στο νερό θα προκαλούσε απώθηση μεταξύ του νομίσματος και του περιβάλλοντος νερού, ωθώντας το νερό μακριά από την πισίνα. Τα κρουστικά κύματα θα αντανακλούν τα σύνορα και το κάτω μέρος της πισίνας, ανεβάζοντας τα επιφανειακά νερά.

Μπορείτε να δείτε στο anime ότι όλες οι εκρήξεις έχουν κάποια κίνηση προς τα πλάγια, αλλά η ΔΕΥΤΕΡΗ έκρηξη που εμφανίζεται έχει μια πολύ ξεχωριστή. πλευρική κίνηση, υπονοώντας ότι η κρούση ωθεί το νερό λίγο και στις πλευρές, καθώς το ηλεκτρικά φορτισμένο νερό απομακρύνεται από το νόμισμα ενώ το νόμισμα διασχίζει την πισίνα.

Το ζήτημα της εξάλειψης της χρέωσης δεν είναι πρόβλημα. Μπορεί να AIM αστραπή, έτσι μπορούμε να υποθέσουμε ότι οι ηλεκτρομαγνητικές δυνάμεις της μπορούν επίσης να αλλάξουν την τάση διακοπής του αέρα γύρω από το νόμισμα (είτε αυξάνοντας την πίεση γύρω από το νόμισμα είτε κάνοντας κενό.

Πρέπει να εξετάσουμε την χωρητικότητα του νομίσματος

Η ακτίνα ενός τετάρτου είναι 13 mm

Με δυναμικό 1 δισεκατομμύριο βολτ, η χρέωση του νομίσματος είναι

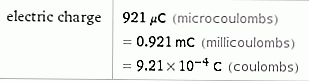
Τώρα, μπορούμε να υπολογίσουμε την ηλεκτρική δύναμη μεταξύ του φορτισμένου νομίσματος και του φορτισμένου νερού, και για λόγους συντομίας, ας υποθέσουμε:

το μισό φορτίο έχει μεταφερθεί στο νερό.
οι τοίχοι και το κάτω μέρος της πισίνας είναι εντελώς απομόνωση και άφθαρτος.
το νόμισμα έχει φτάσει στο κάτω μέρος μόλις μεταφερθεί η μισή χρέωση.
Το νερό απέχει 1 mm από το νόμισμα

Σε αυτήν την περίπτωση, η δύναμη μεταξύ νομίσματος και νερού υπολογίζεται με τον νόμο του coulomb:

Φτάνουμε στο Megajoule εδώ.

Δεδομένης της μάζας του 10% του νερού της πισίνας, αυτή η δύναμη δίνει στο νερό μια στιγμιαία επιτάχυνση:

Τώρα, για να ανυψώσουμε το νερό 100 μέτρα, πρέπει να αποτυπώσουμε το νερό με ταχύτητα 44,3m / s

Έτσι, ο χρόνος αλληλεπίδρασης μεταξύ νομίσματος και νερού πριν η υπόλοιπη ενέργεια διαλυθεί κάνοντας:

Ο Krazer είπε:
ενέργεια που δαπανάται για τη θέρμανση του νερού, δημιουργώντας τους ήχους δυνατή έκρηξη, οποιοδήποτε δραματικό αποτέλεσμα ανέμου

Και αυτό είναι

που αντιπροσωπεύει

Ακόμα κι αν επρόκειτο να λάβετε υπόψη το διασκεδασμό φόρτισης, τη φθίνουσα δύναμη απώθησης μεταξύ του νερού και άλλες μικρές υποθέσεις εδώ, υπάρχει άφθονη ενέργεια για τα πάντα.

Υπάρχει άφθονη ενέργεια παντού για να χρησιμοποιηθεί με όποιον τρόπο θέλετε.

Αλλά νομίζω ότι αυτό εξηγεί ξεκάθαρα από πού προέρχεται η ενέργεια για την ανύψωση του νερού.

Επίσης, εάν λάβετε τα γεγονότα των μεταγενέστερων επεισοδίων, όταν χρησιμοποιεί άλλα αντικείμενα εκτός από ένα νόμισμα

Ένα γιγαντιαίο ρομπότ νύχι και αργότερα ένα ολόκληρο γιγαντιαίο ρομπότ

μπορείτε να δείτε ότι η ποσότητα της αποθηκευμένης ενέργειας είναι μεγαλύτερη, όπως και η καταστροφική δύναμη. Έχει νόημα, επειδή η χωρητικότητα αυτών των αντικειμένων είναι μεγαλύτερη από ένα νόμισμα.

Ευχαριστώ πολύ τον Wolfram Alpha για τους υπολογισμούς και τις εικόνες.

Περισσότερες θεωρίες:

Η ηλεκτρική ενέργεια μπορεί να συνεχίσει την επιτάχυνση του νομίσματος ακόμα και μετά την έξοδο από το "ρύγχος".

Εάν χρεώνει το νόμισμα, μπορεί να δημιουργήσει μια άλλη χρέωση του ίδιου σημείου στον εαυτό της μετά την έξοδο του νομίσματος από το "ρύγχος". Έτσι, ακόμη και αν το νόμισμα φύγει με ταχύτητα 1030m / s, θα μπορούσε να το επιταχύνει ακόμα και μετά την πυροδότηση. Αλλά δεν είναι καν απαραίτητο, γιατί ...

Η περιστροφή του νομίσματος και μία από τις πιο καταστροφικές δυνάμεις: Αρμονικές.

Όπως μπορούμε να δούμε από αυτό το γράφημα wikipedia, μόλις επιτευχθεί ο μέγιστος συντονισμός (1: 1), η μεταφορά ενέργειας αυξάνεται δραματικά. Τα Wind Harmonics είναι αρκετά για να καταστρέψουν μια γέφυρα μετακινώντας την σαν μια σειρά από βιολί. Εάν μπορεί να γυρίσει το νόμισμα έτσι ώστε η συχνότητά του να ταιριάζει απόλυτα με την αρμονική συχνότητα της πισίνας, θα μπορούσε να μεταφερθεί τεράστια ενέργεια.

Μόλις παρατήρησα ότι το νερό θα χρειαζόταν 9 δευτερόλεπτα για να ανεβεί 100 μέτρα στα 44,3 m / s. Δεδομένου ότι η έκρηξη διαρκεί μόνο μερικά καρέ, μπορούμε να υποθέσουμε ότι ο χρόνος επαφής είναι λίγο μεγαλύτερος από 5 ms και το νερό προς τα πάνω αραιώνει / εξατμίζεται αφού χτυπήσει 100 m
Λοιπόν, η πισίνα είναι μόνο ένα παράδειγμα, συχνά βλέπουμε να σταματά και να εκτοξεύει αυτοκίνητα στον αέρα, παράγει αρκετή θερμότητα για να λιώσει δύο διαδοχικές μεταλλικές ράβδους και να αφήσει μια βαθιά γρατσουνιά στη γη στην οποία ταξίδεψε, ακόμα και χωρίς άμεση επαφή. Φαίνεται σαν να υπάρχει άλλη ενέργεια εκτός από την καθαρή ταχύτητα του νομίσματος.
Επίσης για να μην αναφέρουμε ότι στη σειρά Railgun, έδειξε ότι μπορεί να προωθήσει αντικείμενα εκτός από ένα νόμισμα (δηλαδή, έναν τεράστιο βραχίονα ρομπότ και έναν ολόκληρο δορυφόρο) σε παρόμοιες ταχύτητες.

Αν και υποκειμενική, ήταν από την αρχή εντυπωσιακή μου εντύπωση ότι το στοιχείο του βλήματος είναι έμμεσο (και πιθανώς οριακό άσχετο) με την ικανότητά της.

Μπορεί να παράγει πολύ ενέργειας
Η ενέργεια πηγαίνει όπου πηγαίνει το βλήμα
Ωστόσο, δεν αποδεικνύεται ότι το βλήμα μεταφέρει η ενέργεια

Το βλήμα μπορεί να είναι απλά ένας φάρος ή ένας τύπος εστίασης, πιθανώς καθαρά ψυχολογικός (με την τεχνική να είναι αντίθετη από την τυχαία εκτόξευση εκρήξεων ανεξέλεγκτης ηλεκτρικής ενέργειας).

Θυμάμαι ότι πυροβόλησε μεγάλο βλήμα σε μεταγενέστερα επεισόδια, ωστόσο, η παραπάνω κερδοσκοπία μπορεί να εξακολουθεί να ισχύει.

+1, αυτή είναι μια εξαιρετική εξήγηση IMO. Ίσως να υπήρχε μια σκηνή όπου οι άνθρωποι βρίσκουν ένα νόμισμά της, αλλά θυμάμαι ότι πολλές πυρκαγιές της ράγας της είχαν γίνει το νόμισμα μια δέσμη, υποθέτω ότι το λιώνει στη διαδικασία (αν κάτι απομένει καθόλου).
1 Ένας τρόπος για να επαληθευτεί αυτό θα ήταν να δούμε αν χρησιμοποιεί ποτέ κάτι μη μεταλλικό ως βλήμα. Εάν το Railgun της είναι στην πραγματικότητα Railgun με την επιστημονική έννοια, θα πρέπει να ενεργήσει σε κάτι που μπορεί να επιταχυνθεί με ηλεκτρομαγνητισμό, έτσι ένα μέταλλο κάποιου είδους. Εάν μπορεί να χρησιμοποιήσει μη μεταλλικά αντικείμενα, τότε δεν είναι πραγματικά ένα πιστόλι και αυτή η εξήγηση θα ήταν πολύ πειστική.

Υποστηρίζω ότι πρόκειται για μια φυσική Anime με το να απορρίψουμε τις εναλλακτικές δυνατότητες που προτείνατε.

Έχετε δίκιο - η μεταφορά μιας τέτοιας ποσότητας ενέργειας είναι αδύνατη η στιγμή της αδράνειας. Ακόμη και οι υπερδυνάμεις του Misaka είναι ένας κόσμος μακριά από σχετικιστικές ταχύτητες.
Η ενέργεια δεν μπορεί να αποθηκευτεί ως φορτίο στο νόμισμα, καθώς θα συνεχίζει να διαχέεται ως «αστραπή».
Η ενέργεια δεν θα μπορούσε να προέρχεται από μαζική ενέργεια. Εκτός από την θανατηφόρα ακτινοβολία που προκύπτει, η απελευθέρωση μάζας ενέργειας χωρίς χρήση αντιύλης θα σήμαινε απελευθέρωση πυρηνικής ενέργειας. Η πυρηνική ενέργεια μπορεί να απελευθερωθεί μόνο υπό ακραία πίεση (οι πυρηνικές αντιδράσεις σε βόμβες ξεκινούν με συμπίεση του Ουρανίου με την έκρηξη μιας μικρότερης βόμβας). Εάν κάποιος μπορούσε να βρει ένα παράδειγμα της Μισάκα να βρει το νόμισμά της αφού το πυροβόλησε, αυτό θα διαψεύσει σαφώς το επιχείρημα μαζικής ενέργειας.

Τέλος, οι Mythbusters απέδειξαν σε αυτό το βίντεο ότι ένα νόμισμα που ταξιδεύει με 3 φορές την ταχύτητα του ήχου (γύρω από την ταχύτητα μιας σφαίρας) απλώς χάνει το σκυρόδεμα.

Αξίζει επίσης να σημειωθεί ότι (στο βαθμό που θυμάμαι) οι «ψυχικές» δυνάμεις του τύπου που έχει ο Misaka βασίζονται χαλαρά στη διαρκώς δημοφιλή, φανταστική, διπλή παρερμηνεία του πειράματος της σκέψης του Schr's-cater: αυτή η αντίληψη επηρεάζει πραγματικότητα, και έτσι η αλλαγή της αντίληψης με τον σωστό τρόπο θα πρέπει να αλλάξει την πραγματικότητα. (Ή κάτι τέτοιο. Υπήρχε γύρω από το techno-babble, αλλά αυτό φαινόταν να είναι το επίκεντρο του.)

Έτσι, μια εναλλακτική αν και λιγότερο ενδιαφέρουσα εξήγηση των δυσανάλογων επιπτώσεων του railgun της θα ήταν κάτι σύμφωνα με τα εξής: Η αντίληψη της Misaka για το πόσο ισχυρό πρέπει να είναι το railgun είναι λάθος, με αποτέλεσμα υπερβολικά αποτελέσματα.

Όλοι ξεχνάτε το βασικό γεγονός ότι η μέτρηση των 1030 m / s λήφθηκε ενώ πυροβολήθηκε στο νερό. Οι επιδράσεις της έλξης στο κέρμα που εκτοξεύονται στο νερό είναι πολύ μεγαλύτερες σε μέγεθος από τις επιδράσεις της έλξης ενώ πυροδοτούνται μέσω αέρα. Ο αέρας είναι σχεδόν χίλιες φορές λιγότερο πυκνός από το νερό. Εάν εκτελέσουμε την εξίσωση για drag, καταλήγουμε με μέγεθος ισχύος στο νόμισμα των 18.466 Newtons. [18466 = .5 * 1000kg / m ^ 3 * (1030m / s) ^ 2 * .82 * 0.000042455m ^ 2]

0,82 είναι ο συντελεστής οπισθέλκουσας για έναν μακρύ κύλινδρο, όπως ένα arcade νόμισμα, 1000kg / m ^ 3 είναι η πυκνότητα του νερού και .000042455m ^ 2 είναι η διατομή του νομίσματος που πυροδοτείται.

εάν εκτελέσουμε την εξίσωση αντίστροφα για να ανακαλύψουμε την ταχύτητα του νομίσματος στον αέρα, θα μείνουμε με ταχύτητα 29.428m / s.

Ακούγεται πολύ περισσότερο σαν ένα σωστό σιδηροδρομικό όπλο, έτσι δεν είναι;

Το "A tertentu Magical Index" έχει 50 μυθιστορήματα, 13 τόμους manga, 2 σεζόν anime, μια ταινία και μερικά βιντεοπαιχνίδια.

Το «A Scientific Railgun» έχει 2 ελαφριά μυθιστορήματα, 11 τόμους manga, 2 εποχές anime, ένα OVA και ένα δικό του βιντεοπαιχνίδι.

Σε καμία από αυτές τις πηγές (που θυμάμαι, ούτως ή άλλως) δεν είναι το κόλπο του πιστόλι της Misaka που υπονοείται ότι είναι κάτι άλλο εκτός από ένα διακριτικό arcade (όχι ένα νόμισμα, γι 'αυτό και είναι αρχικά σιδηρούχο) να ταξιδεύει τρεις φορές την ταχύτητα του ήχου.

Και υπάρχει μια άλλη παράξενη ιδιότητα της επίθεσης σιδηροδρομικού - η Τούμα, το αγόρι με την αντι-μαγική γροθιά, μπορεί να το πιάσει. (Όπως φαίνεται στο κεφάλαιο 7, τόμος 1 του Railgun manga.)

Δεδομένου ότι η Τούμα μπορεί να το διαλύσει, αυτό σημαίνει ότι υπάρχει ακόμα κάτι υπερφυσικό για το νόμισμα, ακόμη και όταν λιώνει. Αυτή η υπερφυσική ιδιότητα θα είναι ο λόγος που έχει μια ώθηση που ξεπερνάει αυτό που θα έπρεπε να έχει μόνο στην ορμή.

Δεν έχω κανένα αποδεικτικό στοιχείο για το επόμενο σημείο μου, αλλά πιστεύω ότι το μαγνητικό πεδίο της Misaka συνεχίζει απλώς να ωθεί το νόμισμα καλά αφού αφήσει το χέρι της. Αυτό θα εξηγούσε και τις δύο παραξενιές.

Ας μην ξεχνάμε στο επεισόδιο που έκανε το βραχίονα ρομπότ που το έκανε επειδή το άτομο καθόταν έξω από το εύρος των νομισμάτων της. Στο τέλος της δέσμης δεν είχε απομείνει νόμισμα. Εξήγησε καθώς μπλοκάρει, πιάστηκε και πυροβόλησε τον εν λόγω βραχίονα ότι υπάρχει λόγος που συνήθως χρησιμοποιεί νομίσματα.

Υποψιάζομαι ότι πολλοί παράγοντες συνδυάζονται για να συμβάλουν στο καταστροφικό δυναμικό της, συμπεριλαμβανομένης της καθορισμένης κατάστασης badass, της συνεχιζόμενης επιτάχυνσης, της αδράνειας, της περιστροφής, του υπερηχητικού σοκ και της πιθανής μετατροπής της ύλης σε πλάσμα.

Θυμηθείτε ότι πιθανότατα εκτρέπει την ενέργεια για να καταπολεμήσει την ανάκρουση και άλλες καταστροφικές πτυχές του πυροβολισμού του σιδηροτροχιού. Αυτή η θωράκιση είναι αρκετή για να σταματήσει πολλές κατευθυνόμενες πυρηνικές εκρήξεις ικανές να λιώσουν γρήγορα μέσω σκυροδέματος και χάλυβα, παρά το γεγονός ότι ο Misaka είχε εξαντληθεί τότε. Είμαι βέβαιος ότι αυτή η ενέργεια μπορεί να προκαλέσει δευτερογενή επιτάχυνση.

Είναι μια περίπτωση της φυσικής του anime, όπως ανέφεραν άλλες αφίσες αλλά όχι η μέση φυσική σας anime, λέγεται σε ορισμένα μέρη του ευρετηρίου της σειράς manga και της αδερφής ότι ο τρόπος λειτουργίας των esper power είναι να χειριστεί ένα πεδίο στρέβλωσης της πραγματικότητας ώστε να ταιριάζει στυλ των εξουσιών τους. Ως εκ τούτου, το σιδηροδρομικό όπλο του misaka λειτουργεί επειδή έχει αρκετή ενέργεια στρεβλώνοντας ενέργεια και μαθηματικά πίσω από αυτό